王葳翔 第九周進度 Transition state structure
•Please use ChatGPT to explore a thematic series of questions within the scope of computational chemistry and follow up with further inquiries about any unfamiliar terms ( except homework )
•Find the transition state structure and calculate the barrier height (ΔV≠) for the following reaction.
reaction:HNC → HCN
| MP2/aug-cc-pvtz | E(Hartree) | ΔV≠(Hartree) | ΔV≠(kcal/mol) |
| HCN | -93.25869 | 0.05483 | 34.4 |
| HNC | -93.23131 | ||
| TS | -93.17648 | ||
| MP2/6-31+G** | E(Hartree) | ΔV≠(Hartree) | ΔV≠(kcal/mol) |
| HCN | -93.17164 | 0.05605 | 35.2 |
| HNC | -93.14306 | ||
| TS | -93.08701 |
transition state structure
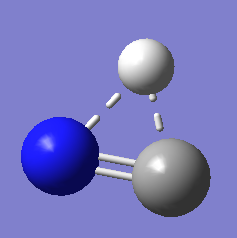
methods : MP2/aug-cc-pVTZ、MP2/6-31+G**
•Calculate the k(rate constant) at different temperatures (at least 3 different temperatures) for the following reaction and plot of ln(k) versus 1000/T then compare with the experimental values.
reaction:CH4 +OH․→ H2O + CH3․
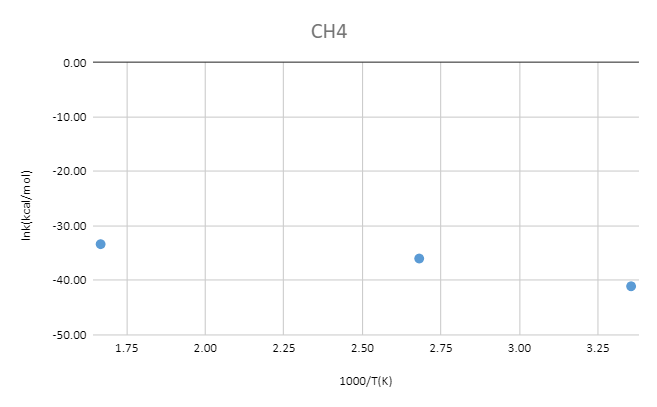
MP2/6-31+G**
| T(k) | CH4(Hartree) | OH-(Hartree) | TS(Hartree) | ΔG‡(kcal/mol) | 1000/T(K) | k(kcal/mol) | lnk(kcal/mol) |
| 298 | -40.33935 | -75.54838 | -115.86331 | 15.32 | 3.36 | 1.46E-18 | -41.07 |
| 373 | -40.35605 | -75.56385 | -115.88617 | 21.17 | 2.68 | 2.37E-16 | -35.98 |
| 600 | -40.36340 | -75.57278 | -115.90464 | 19.79 | 1.67 | 3.32E-15 | -33.34 |
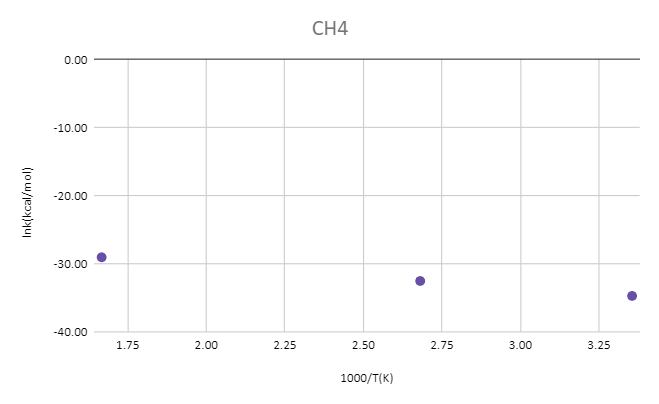
MP2/aug-cc-pvtz
| T(k) | CH4(Hartree) | OH-(Hartree) | TS(Hartree) | ΔG‡(kcal/mol) | 1000/T(K) | k(kcal/mol) | lnk(kcal/mol) |
| 298 | -40.38645 | -75.63468 | -116.00322 | 11.56 | 3.36 | 8.39E-16 | -34.71 |
| 373 | -40.39184 | -75.63982 | -116.01135 | 13.01 | 2.68 | 7.53E-15 | -32.52 |
| 600 | -40.40958 | -75.65641 | -116.03872 | 17.34 | 1.67 | 2.45E-13 | -29.04 |
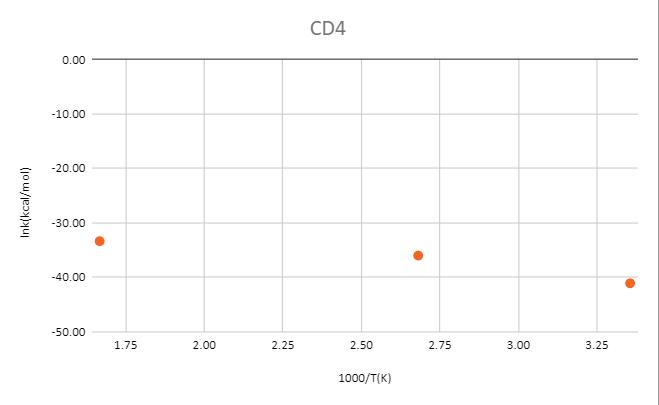
reaction:CD4 +OH․→ H2O(1 H will replace by D) + CD3․
MP2/6-31+G**
| T(k) | CD4(Hartree) | OH-(Hartree) | TS(Hartree) | ΔG‡(kcal/mol) | 1000/T(K) | k(kcal/mol) | lnk(kcal/mol) |
| 298 | -40.35064 | -75.54838 | -115.87318 | 15.32 | 3.36 | 1.46E-18 | -41.07 |
| 373 | -40.36686 | -75.56385 | -115.89568 | 21.17 | 2.68 | 2.37E-16 | -35.98 |
| 600 | -40.37403 | -75.57278 | -115.91371 | 19.79 | 1.67 | 3.32E-15 | -33.34 |
| T(k) | CD4(Hartree) | OH-(Hartree) | TS(Hartree) | ΔG‡(kcal/mol) | 1000/T(K) | k(kcal/mol) | lnk(kcal/mol) |
| 298 | -40.40541 | -75.63468 | -116.00456 | 11.56 | 3.36 | 8.39E-16 | -34.71 |
| 373 | -40.41619 | -75.63982 | -116.01845 | 13.01 | 2.68 | 7.53E-15 | -32.52 |
| 600 | -40.42645 | -75.65641 | -116.04038 | 17.34 | 1.67 | 2.45E-13 | -29.04 |
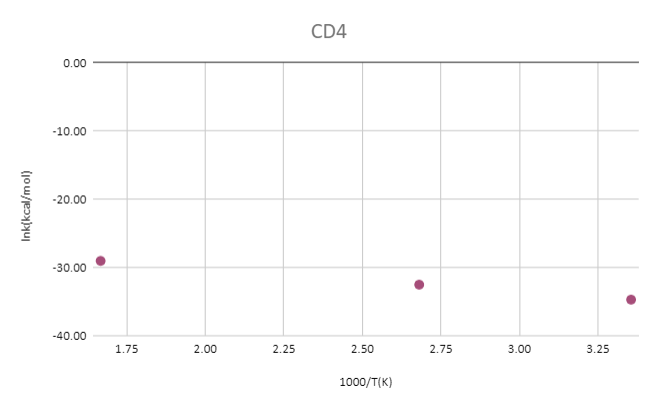
The results show that the barrier heights and rate constants of the reactions depend on the choice of methods and basis sets.
For the HNC → HCN reaction, the MP2/aug-cc-pvtz method gives lower barrier heights and higher rate constants than the MP2/6-31+G** method.
For the CH4 + OH․→ H2O + CH3․ reaction, the MP2/aug-cc-pvtz method gives higher barrier heights and lower rate constants than the MP2/6-31+G** method.
The plots of ln(k) versus 1000/T show linear relationships for both reactions and both methods, indicating that the Arrhenius equation is valid. The slopes of the plots are proportional to the activation energies, and the intercepts are proportional to the pre-exponential factors.
